| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 3d
- 딥러닝
- FineGrained
- PRML
- nlp
- Depth estimation
- Front
- GAN
- computervision
- SSL
- CV
- Torch
- 알고리즘
- 머신러닝
- web
- classification
- REACT
- dl
- Vision
- FGVC
- math
- Meta Learning
- 자료구조
- clean code
- cs
- ML
- nerf
- algorithm
- pytorch
- Python
- Today
- Total
KalelPark's LAB
[ PRML ] Ch2-1 supplementary materials 본문

포아송 분포(Poisson Distribution)
어떤 단위 구간(시간)에서 일어나는 특정 사건의 발생 횟수 분포에 대한 것을 의미합니다. 즉, 포아송 분포를 통하여, 평균 발생 횟수가 5개가 되는 단위 구간에서 사건이 3개 일어날 확률은 어느정도가 되는지 구할 때 사용합니다. 해당 구간 내 사건은 랜덤으로 일어나므로 정확한 타이밍은 예측하는 것이 불가능합니다.
* 포아송 분포(Poission distribution)을 따른다면, 다음의 성질을 만족해야 합니다.
1. 서로 겹치지 않는 단위 구간에서 발생하는 사건들은 서로 독립이다.
2. 단위 구간의 크기 대비 사건의 평균 발생 횟수의 비율은 일정하다.
3. 같은 사건이 동시에 일어날 확률은 0이다.


* 여기서 눈여겨볼 점은 포아송 분포는 기댓값과 분산이 서로 같다는 것입니다.

여기서 적률 생성함수(Moment Generating Function)란?
- 수리통계학에서는 주로 나오는 용어이다. (적률 과 생성함수를 이어 붙어서 만든 말이다.) * 자세한 내용은 하단의 링크를 참고하자.
1. 적률은 평균이나, 분산 등을 포괄하는 추상적인 개념이다. 적률은 차수에 따라 적절한 조작을 거쳐 의미 있는 통계량이 될 수도 있지
만, 그 자체로는 통계적인 의미를 갖지 않는다. 무리하게 어떤 통계량과 연결 시키지 말고 적률 그 자체로 알아도 충분하다.
2. 생성함수는 다항함수의 일반적인 꼴로 변경해주는 것을 의미합니다. 매클로린 전개를 활용하면, 됩니다. 생성함수는 다항함수를 일반
적인 꼴로 나타낸 것에 지나지 않습니다.
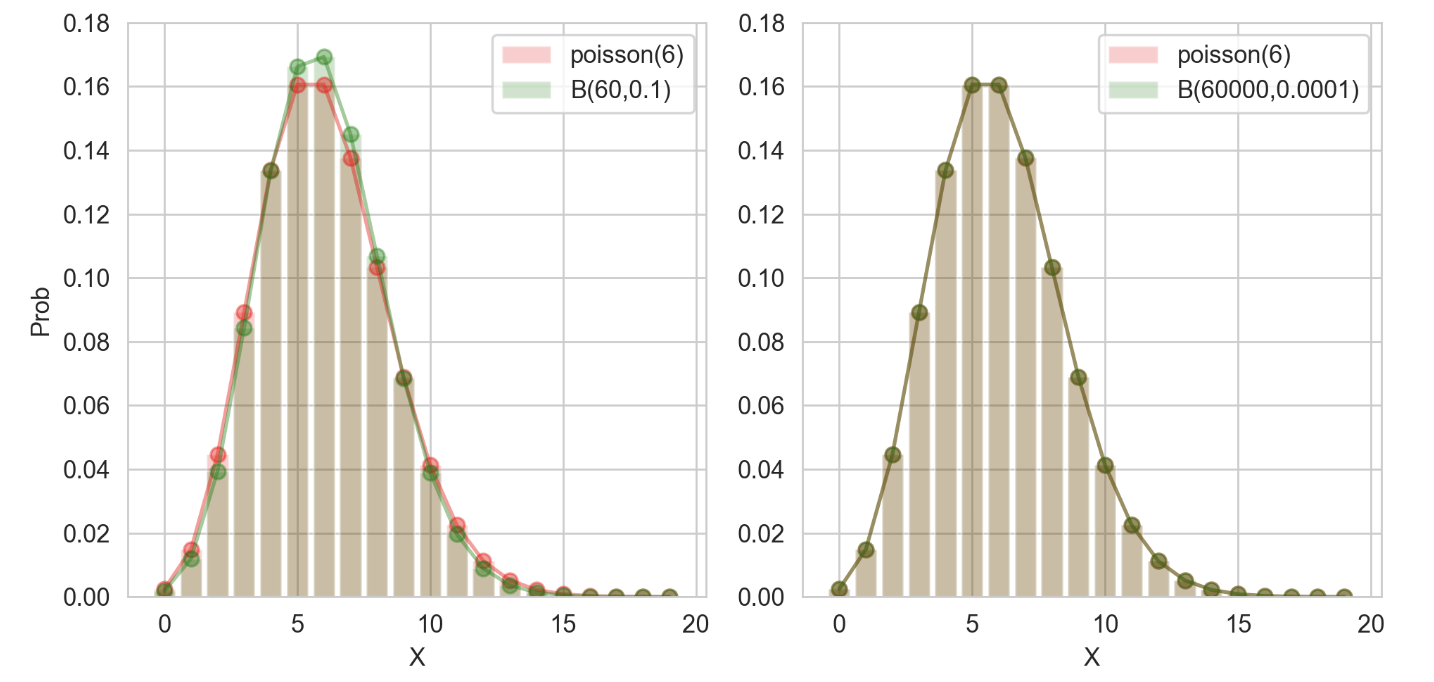
이항 분포(Binomial Distributuion)의 포아송 분포(Poisson Distribution)
이항 분포의 경우, n이 조금만 커져도 계산하는 과정이 정말 복잡해집니다. 만약 시행횟수가 높지만, 성공 확률은 낮다면, 이것을 평균을 이용하면 포아송 분포를 이용하면 되는 것입니다. 즉 포아송 분포는 시행횟수가 측정이 불가할 정도로 클 경우에 평균 성공 횟수만 알면 이용가능합니다.
지수 분포(Exponential Distribution)
특정한 사건이 일어나고, 다음에 같은 사건이 일어날 때까지 걸리는 시간에 대한 분포입니다. 예를 들어, 평균적으로 10분마다 도착하는 버스가 있을 때, 버스를 놓친 후 그 다음 버스가 올때까지 기다리는 시간은 지수분포를 따릅니다.
그렇다면, 기다리는 시간을 알고자 할 때, 시간 단위에서 사건이 평균적으로 몇번 발생하는지를 알아야 합니다.
즉, 사건의 발생 횟수를 바탕인 분포인 포아송 분포에서 사건 사이의 대기 시간은 지수 분포를 따른다고 말할 수 있습니다.
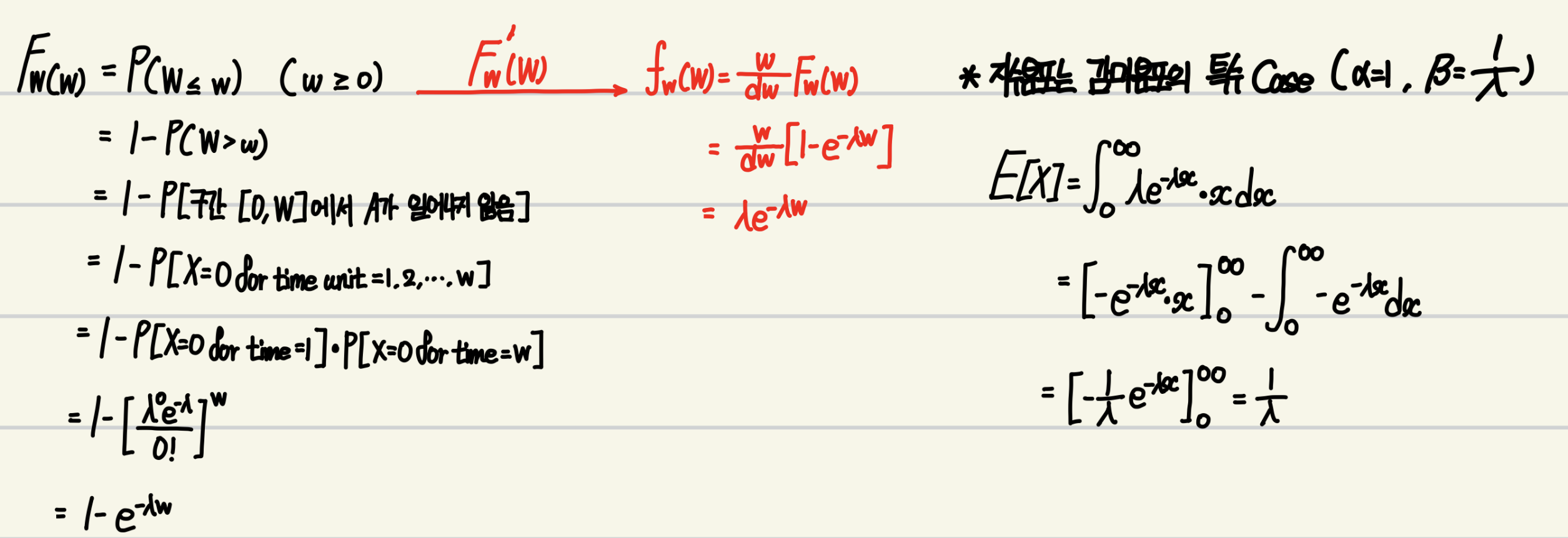
* 위의 식을 미분하면, pdf를 구할 수 있습니다.
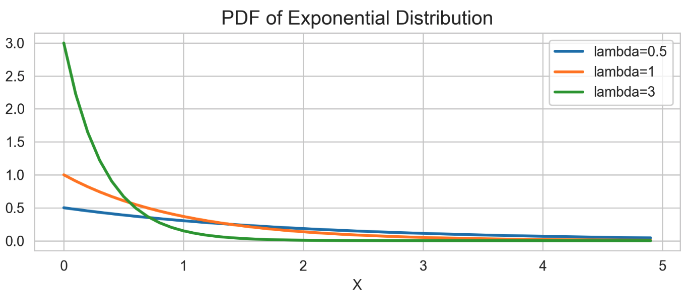
추가로, 지수 분포는 감마 분포의 특수한 경우입니다. α=1, β=1 / λ 인 감마 분포라는 것을 이용하면 기대값 및 분산을 쉽게 구할 수 있습니다. 어떤 사건이 평균 발생 수가 λ인 포아송 분포를 따를 때, 사건 사이의 평균 소요 시간은 그것의 역수 1/λ가 됩니다. 어떤 사건의 평균 발생 건수가 4라고 합시다. 즉, 특정 단위 시간에서 사건이 4번 일어나는 거니까, 평균적으로 한 사건이 일어나고 그 다음 사건이 일어나기까지 그 시간 단위의 1/4배 만큼의 시간이 소요된다는 것을 의미합니다.
(하단의 그래프를 보면 낮은 소요 시간 시, 확률 값이 높음을 알 수 있습니다.)
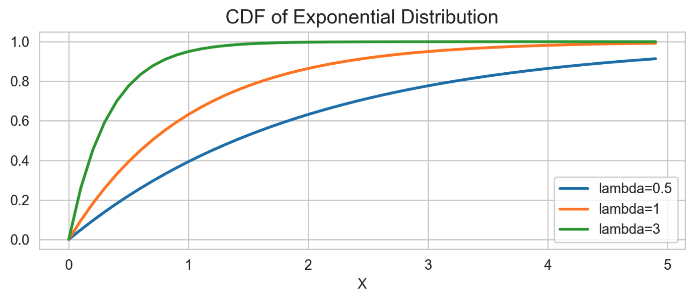
무기억성 (Memoryless Property)
지수 분포하면 빼 놓을 수 없는 성질이 바로 무기억성이다. 다음의 식을 만족하면 무기억성 성질을 가진다고 말합니다.
"무기억성"의 의미는, 어떤 시점부터 소요되는 시간은 과거 시간에 영향을 받지 않는다는 것입니다.
예시를 들면, 어떤 배터리를 한 달간 사용했을 때, 남은 배터리 수명은 한 달 간 사용했던 것에 영향을 받지 않고, 새로운 배터리의 수명과 같다는 것을 의미합니다. 하지만, 일상생활과 관련하여 본다면 비합리적으로 보일 수 있습니다. 실제로 Exponential distribution은 상당히 모델링을 단순화하는 것으로 볼 수 있습니다. 그리하여, 위험률(hazard rate)이 일정한 것보다는 와이블(Weibull distribution)이 훨씬 유연하게 사용될 수 있습니다.
Reference
https://freshrimpsushi.github.io/posts/moment-generating-function/
적률생성함수란?
Moment generating Function
freshrimpsushi.github.io
https://soohee410.github.io/discrete_dist3
[이산형 분포] 포아송 분포(Poisson distribution)
[이산형 분포] 포아송 분포(Poisson distribution) Published Apr 21, 2020 <!-- --> 이번 포스트에서는 포아송분포(Poisson Distribution) 에 대해 알아보고, 이것의 기대값, 분산, 적률생성함수를 구해보겠습니다. 나
soohee410.github.io
http://norman3.github.io/prml/docs/chapter02/1
1. Binary Variables
1. Binary Variables 우선 가장 간단한 형태의 식으로 부터 논의를 시작한다. 랜덤 변수 \( x \) 가 \( x \in \{ 0,1 \} \) 인 상황(즉, 취할 수 있는 값이 단 2개)에서의 확률 분포를 살펴본다. 가장 간단한 경
norman3.github.io
https://freshrimpsushi.github.io/posts/moment-generating-function/
적률생성함수란?
Moment generating Function
freshrimpsushi.github.io
'Data Science > PRML' 카테고리의 다른 글
| [ PRML ] Ch2 - 2. Multinomial Variables (0) | 2023.05.07 |
|---|---|
| [ PRML ] Ch2-1 Binary Variables (2) (0) | 2023.05.06 |
| [ PRML ] Ch2-1 Binary Variables (1) (0) | 2023.05.06 |
| [ PRML ] Ch1. The Infomation Theory (0) | 2023.05.05 |
| [ PRML ] Ch1. The Decision Theory (0) | 2023.05.04 |




