| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- FGVC
- Front
- pytorch
- CV
- 3d
- 자료구조
- nlp
- cs
- algorithm
- Vision
- classification
- 알고리즘
- web
- ML
- Torch
- nerf
- REACT
- FineGrained
- math
- clean code
- 딥러닝
- GAN
- 머신러닝
- Python
- Depth estimation
- SSL
- Meta Learning
- computervision
- dl
- PRML
- Today
- Total
KalelPark's LAB
[ PRML ] Ch1. The Infomation Theory 본문

Information Theory
- 어떤 이산 랜덤 변수 x가 있다고 하자.
- 우리가 x의 구체적인 값을 관찰하는 경우 얼마만큼의 정보(information)을 얻는지를 정량화하는 것이 가능합니다.
* 정보(Information)은 "학습에 있어 필요한 놀람의 정도(degree of surprise)"로 해석하면 된다.
* 정보의 양을 h(x)라고 정의한다면, 정의는 결국 확률 함수의 조합으로 표현이 되게 될 것이다.

위의 내용을 정리하자면, 이산확률변수에서는 Non-uniform 분포에서는, Uniform 분포보다 엔트로피가 낮다고 설명하는 것이 가능합니다. 반면에, 연속확률변수에서는 정규분포가 엔트로피를 최대로 만들어냅니다.


Relative Entropy and Mutual Information Theory
Pattern Recognition으로 살펴보자면, 데이터의 실 분포 p(x)가 있고, 예측한 분포 q(x)가 있다고가정을 하자.
q(x)의 코딩 scheme으로 Encoding하여, 데이터를 전송한다고 가정해보자.
이러면, 데이터의 실 분포인 p(x)에 의해, 얻을 수 있는 정보량과 실제 사용한 q(x)의 정보량은 다를 수 있을 것이다.
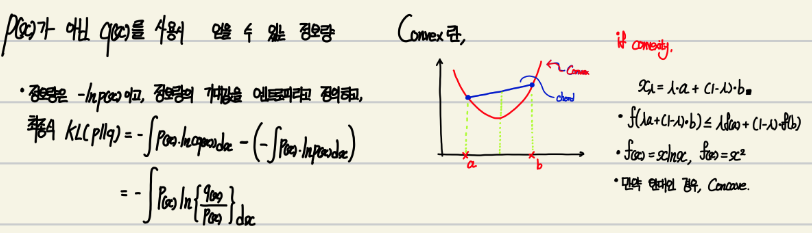
Data Compression
가장 효율적인 압축은 데이터의 실 분포를 정확히 알고 모델을 만들었을 때이다. 실 분포와 다른 분포가 사용되면, KL 만큼의 추가 정보가 만들어지거나, 덜 효율적인 인코딩이 이루어진다.
예를 들어, 모델링하고자 하는 확률분포 p(x)를 따르는 데이터를 생성한다고 가정하자. 이후 만들고자 하는 분포는 조정 가능한 파라미터 0를 이용하여, 만든 q(X|0) 분포이다. 이러한 경우 KL divergence를 최소화하는 0가 결정되어야 합니다.


'Data Science > PRML' 카테고리의 다른 글
| [ PRML ] Ch2-1 supplementary materials (0) | 2023.05.06 |
|---|---|
| [ PRML ] Ch2-1 Binary Variables (1) (0) | 2023.05.06 |
| [ PRML ] Ch1. The Decision Theory (0) | 2023.05.04 |
| [ PRML ] Ch1. The Curse of Dimensionality, The Decision Theory (0) | 2023.05.03 |
| [ PRML ] Ch1. Probability Theory, Model Selection (0) | 2023.05.02 |




