[ PRML ] Ch2-1 Binary Variables (1)

Binary Variables

랜덤 변수 x 가 x ∈ {0,1} 인 상황(즉, 취할 수 있는 값이 단 2개)에서의 확률 분포를 살펴본다.
예를 들어, 동전의 앞, 뒷면이 나올 확률이 서로 동일하지 않다고 가정 시, 확률은 p( x = 1 | μ ) = μ 로 표현할 수 있다.
반대의 경우도, p ( x = 0 | μ ) = 1 − μ 이다.
이를 하나의 표현식으로 합쳐 만들어내면 다음과 같이 기술할 수 있다. Bern(x|μ)=μ^(x)(1−μ)^(1−x)로 표현 가능하다. (Bernoulli)

베르누이 확률변수는, 표본 데이터가 하나 뿐일때 사용되고, 표본 데이터가 여러 개 존재한다면 이항 분포(binominal distribution)를 따릅니다. 

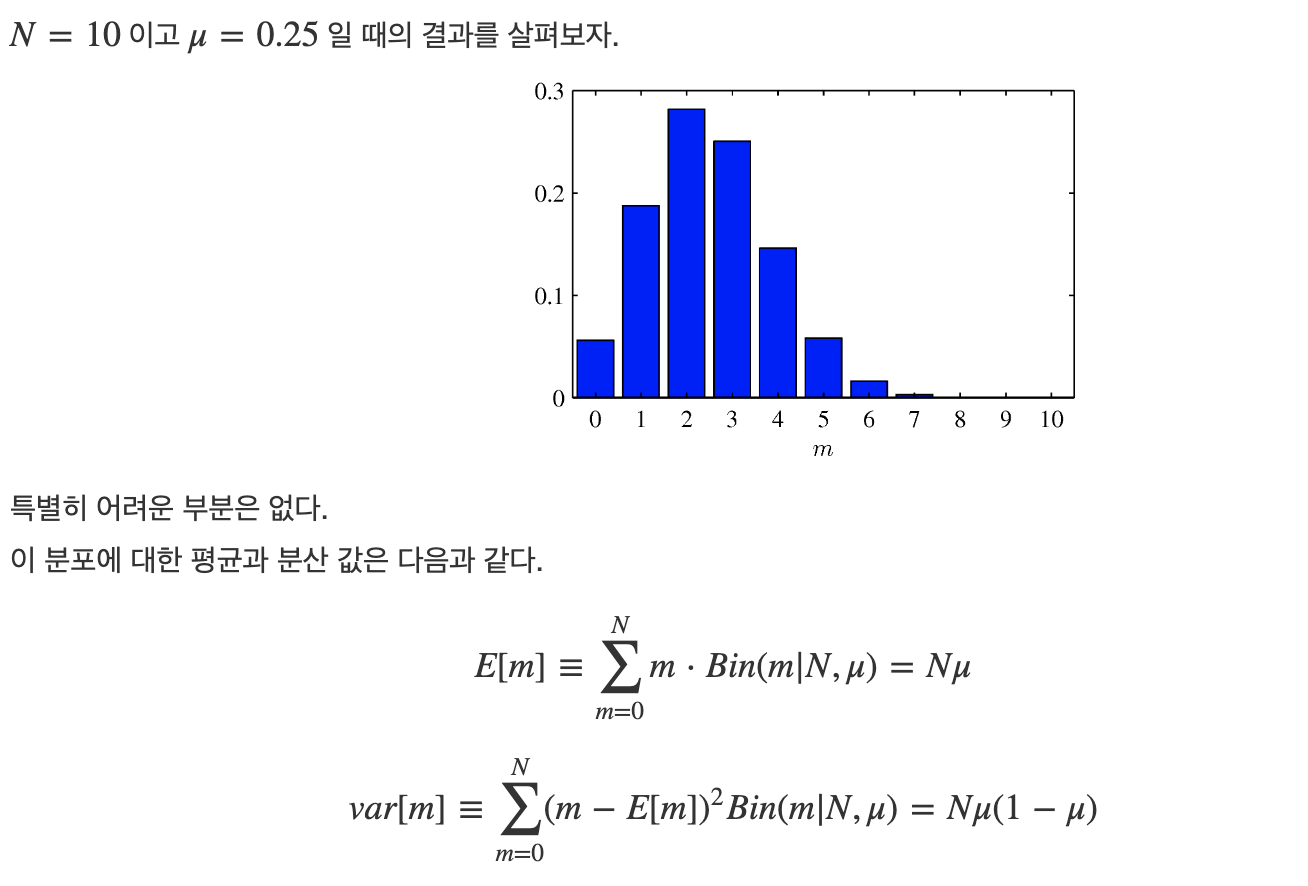
* 이후 베타 분포를 설명하지만, 베타 분포를 알기전, 포아송 분포, 감마 분포, 지수 분포에 대한 이해가 필요하기에 해당 부분부터 살펴보도
   록 하겠습니다.

 

Reference

https://datalabbit.tistory.com/43