| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
- Vision
- Front
- nerf
- dl
- pytorch
- GAN
- nlp
- 머신러닝
- 알고리즘
- cs
- ML
- computervision
- 딥러닝
- CV
- math
- Torch
- Meta Learning
- REACT
- clean code
- 자료구조
- web
- FGVC
- 3d
- FineGrained
- SSL
- Depth estimation
- PRML
- Python
- classification
- algorithm
- Today
- Total
KalelPark's LAB
[Math] chapter 3.4 [Structure-from-Motion: Bundle Adjustment] 본문
[Math] chapter 3.4 [Structure-from-Motion: Bundle Adjustment]
kalelpark 2023. 4. 8. 14:45
Bundle Adjustment
카메라의 이미지 data들로부터 3차원 공간으로 이미지에 나타난 정보들을 모델링을 진행할 때, 카메라의 pose와 3차원 공간의 points들의 위치를 추정할 때 필요한 최적화 기법 중 하나이다.
3D Reconstruction을 진행할 때, Lidar나 Depth Camera같은 거리 값을 이용하는 것이 아니라 2D image들의 묶음으로만 3D 복원을 진행합니다. 보통 SIFT와 같은 특징점을 찾는 알고리즘을 이미지에서 수행하고, Triangulation과 같은 과정을 거쳐, Point들이 어디에 위치하고 있는지 추정을 합니다.


Bundle Adjustment는 Bundle Block Adjustment라고도 불리는데, 이러한 이유는 Block 단위로 수행하여, 많은 이미지 쌍을 동시에 고려하여 최적화를 수행하기 때문이다.
Bundle Adjustment 과정
우선, 이미지에서 특징점을 추출해야 합니다. 어떤 특징점 알고리즘을 사용하는지는 상관이 없습니다. 특징점을 추출하는 방법론(SIFT, SURF, ORB)으로 3D Reconstructure을 진행합니다.
Non-linear square 방법을 사용하기 때문에, 초기값이 존재해야 합니다. 초기 값으로 6-DOF camera pose와 3D point를 정의한 후, 해당 point에 투영하는 과정을 거칩니다. 3D point들을 이미지로 투영을 시키게 된다면, 이미지상에 투영된 점들이 어느 위치에 있는지 계산하는 것이 가능합니다.
계산된 값과 실제로 Measurement들을 활용해서 얼마나 차이가 있는지 계산하는 것이 가능합니다. 이러한 오차를 줄이는 과정이 Bundle Adjustment과정입니다. 오차는 Reprojection error라고 합니다.
즉 과정을 정리하자면,
1. 이미지에서 특징점을 추출합니다. (SIFT) 이후 -> 3차원 공간에 특징점들의 실제 위치를 추정
2. 6-DOF camera pose와 3D points들의 위치의 초기값을 지정
3. 이미지에서 투영된 점들의 위치와 실제 위치를 활용해서 Reprojection error를 추정합니다.
4. Reprojection Error를 최소화할 때는, Non-linear square을 진행합니다.
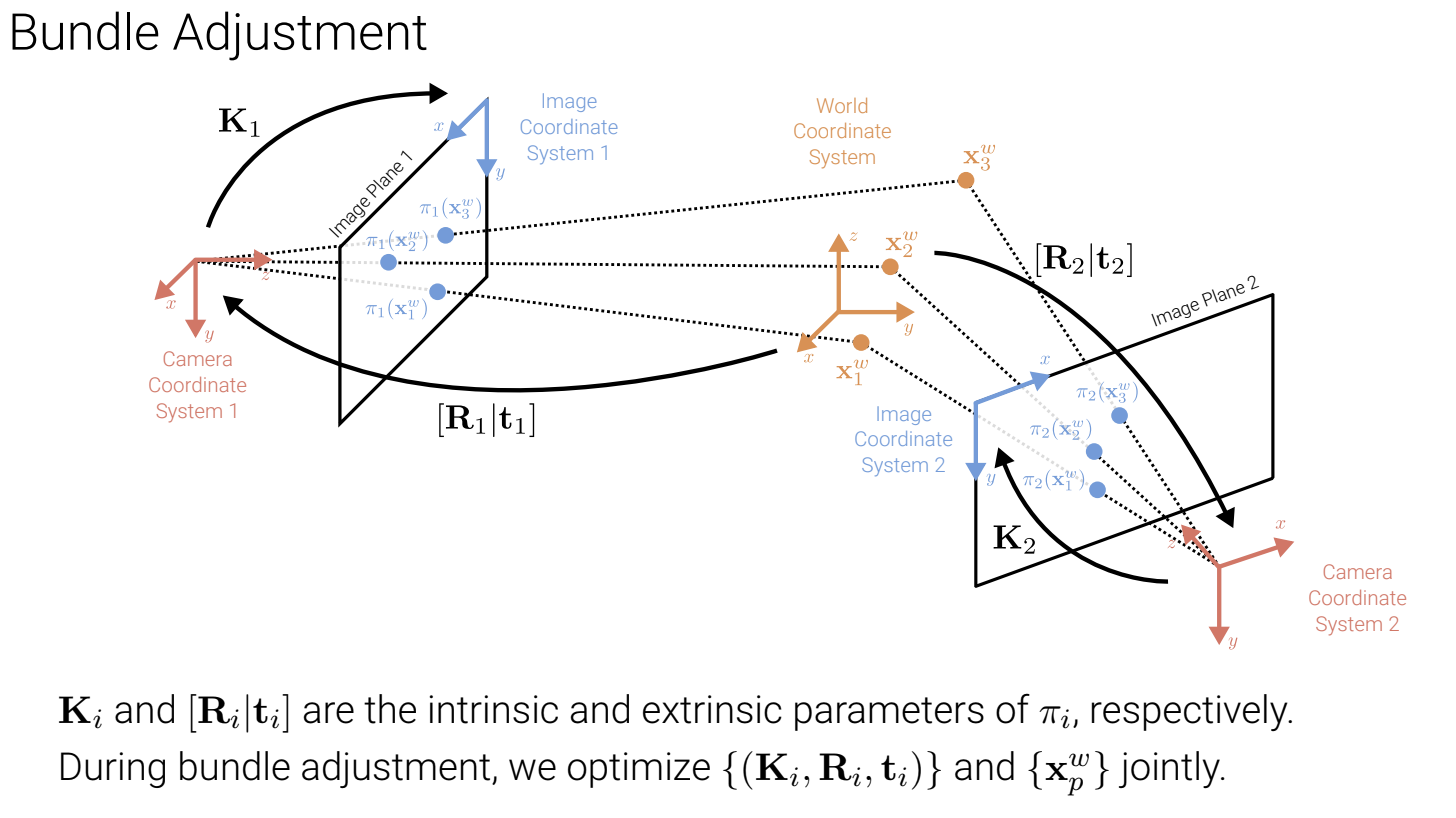
* bundle adjustment 시에는, K 와 [R|T] 그리고, x 좌표 값을 동시에 최적화를 진행합니다.
Uncertainty in the image coordinates란 특징점을 얼마나 추줄했는지 나타내기 위해서 사용합니다.


Known Data association을 가정하는데, Known Data association이란 3D point를 이미지에 투영할 때, 어떤 특징점과 매칭이 되고 있는지 파악하기 위해서 사용됩니다.
Data association을 확실하게 알고 있어야, Bundle Adjustment도 잘 수행하고, 정확한 Data association을 찾는 것이 가능합니다.
3D location of new point X는 x, y, z 3개의 파라미터가 존재하고, scale factor는 1개의 파라미터, 6D exterior orientation은 extrinsic parameter를 의미합니다. 5D projection parameter는 intrinsic parameter를 의미하고, q는 1~2개의 parameter를 사용합니다.
여러가지 카마레를 활용하기 때문에, 카메라마다, 각기 다른 calibration을 적용하여, 그에 맞는 parameter를 찾는 것이 중요합니다.


먼저, x 좌표 y 좌표, 10000개의 이미지, 1000개의 특징점이 있으므로, Observation의 크기는 2 * 10000 * 1000 이 존재합니다.
또한, unknown parameter는 1000개의 특징점에 대한 3DOF, 10000개의 scale factor, 1000개의 카메라에 대한 6DoF를 모두 합한 값입니다. 그러므로 상당히 많은 parameter를 알아야 합니다.
우선, Parameter를 줄이기 위해서, scale factor를 제거합니다. Homogenous coordinates를 사용하는 대신, Euclidean을 사용하면, scale factor를 제거하는 것이 가능합니다.
Bundle Adjustment 특징
statistically optimal solution이라는 특징이 존재합니다. 즉, 우리가 세운 가정이 실제 상황에 잘 부합하는 경우 최적의 해를 찾을 수 있다는 것입니다.
최적의 해를 찾기 위해서는 Data association을 잘 수행하고, uncertainties, correlation도 잘 고려해야 하며, Gaussian noise model을 따라야, 초기값도 잘 찾아야 합니다.

카메라 이미지만으로, 3D reconstruction을 진행하면, "photogrammetric model"을 얻을 수 있는데, 이는 정확한 scale을 고려하지 않습니다. 고려해야 할 것으로는..
Absolute Orientation Through Control Points & Initial Guess & Quality of the Results
Absolute Orientation이란, 3D points의 집합을 정렬할 때, Scale까지 고려해서 Transformation을 결정합니다.
Control Point 정보를 활용하면, 실제 scale까지 고려해서 3D reconstructure을 진행할 수 있습니다.


Direct method란 초기값 없이 Orientation을 구하는 방법입니다. N개의 이미지들에 대한 Direction Solution이 없기 때문에, 이미지 쌍을 쪼개어 orientation을 구하는 방법입니다.
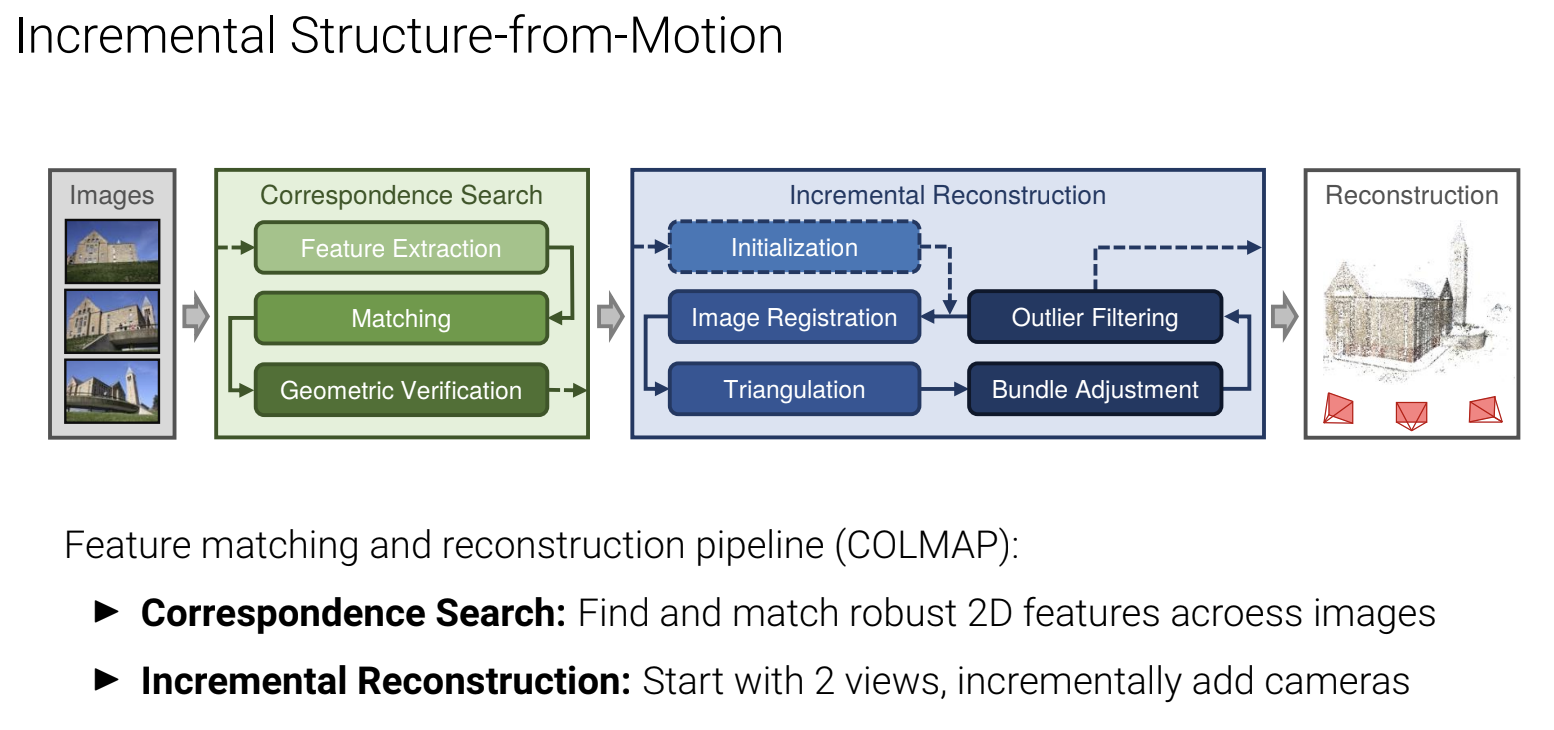
Incremental Structure-from-Motion
COLMAP의 과정을 설명합니다. (추후 작성 예정)
- Correspondence Search : 십자형 2D image로부터 robust feature를 찾습니다.
- Incremental Reconstructure : 2가지 view를 파악합니다.

Feature Matching & Geometric Verification
Overapping된 Image 쌍을 찾고, 관련된 feature들을 얻습니다.
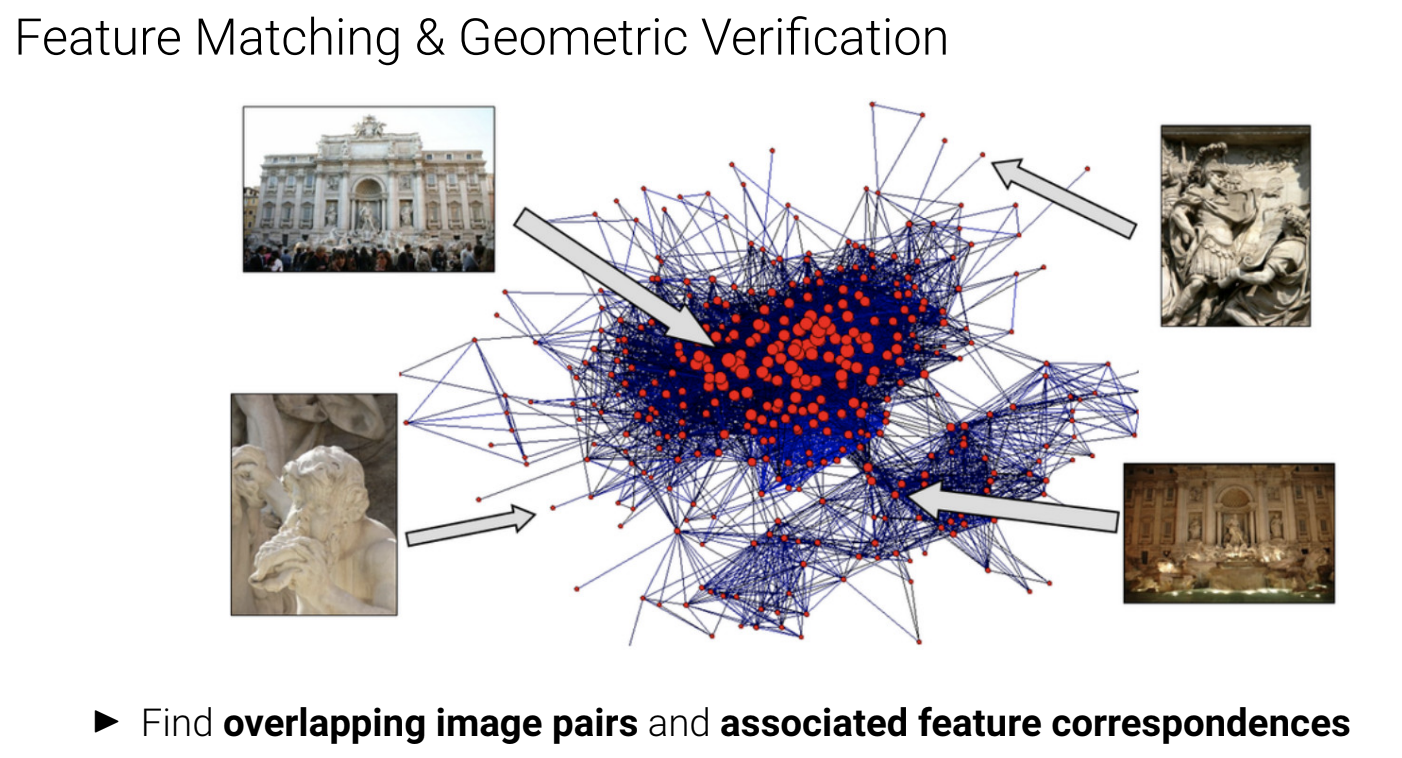
Image Registration
- 영상 정합이란, 현재 Set에 대응하는 새로운 이미지를 찾고, camera pose를 추정합니다.
3D 좌표를 2D 좌표로 대응하는 방법에 대해서 설명하고 있습니다.

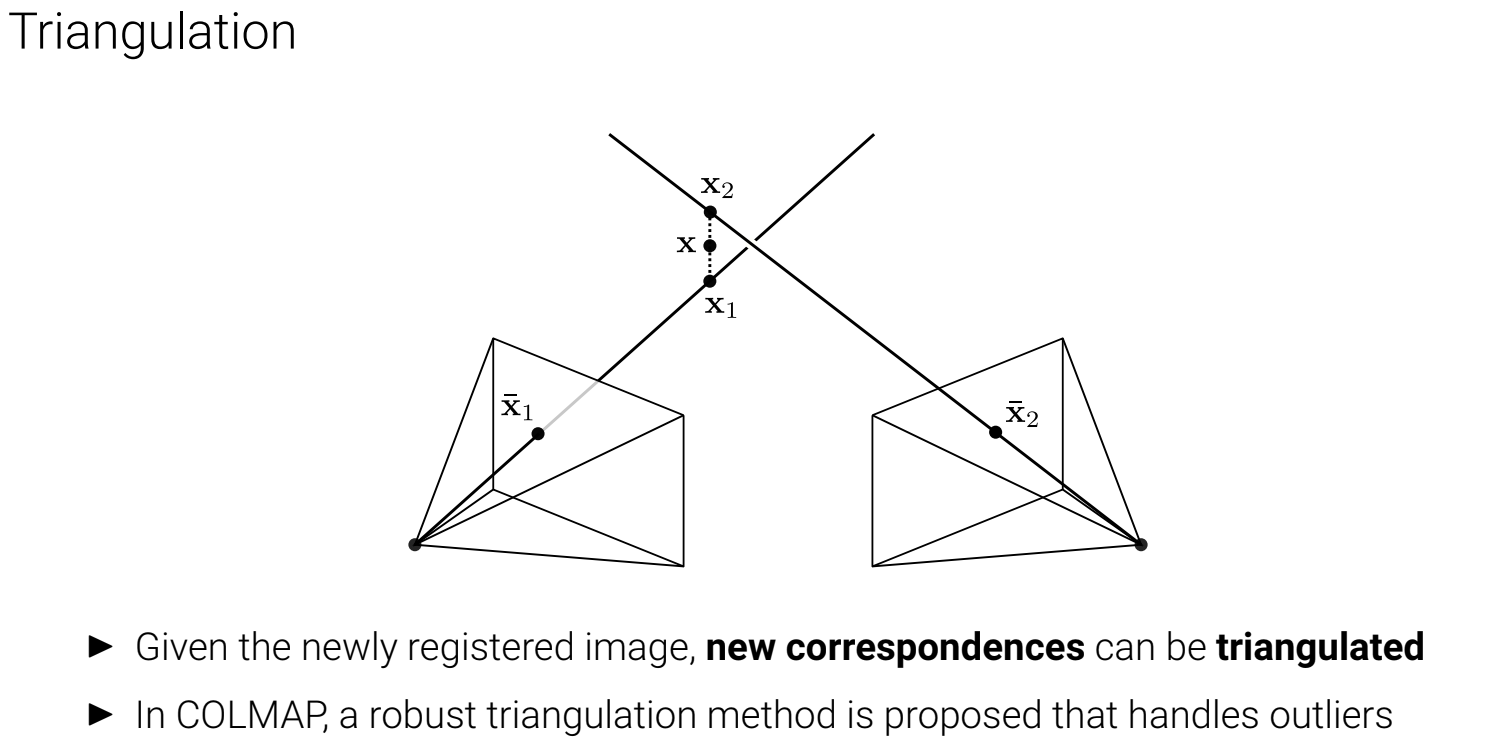
Outlier를 제거하고, Bundle Adjustiment를 하는 과정이다. 위에서 소개한 내용입니다.

Result


Reference
'Study > Math' 카테고리의 다른 글
| [Math] chapter 4.1 [Stereo Reconstruction] - supplementary (0) | 2023.04.09 |
|---|---|
| [Math] chapter 4.1 [Stereo Reconstruction] (0) | 2023.04.09 |
| [Math] chapter 3.3 [Structure-from-Motion: Factorization] (0) | 2023.04.07 |
| [Math] chapter 3.2 [Structure-from-Motion: Two-frame Structure-from-Motion] (0) | 2023.04.07 |
| [Math] chapter 3.1 [Structure-from-Motion: Preliminaries] (0) | 2023.04.06 |




