Recent Posts
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
Tags
- math
- ML
- dl
- Meta Learning
- 3d
- pytorch
- FineGrained
- clean code
- SSL
- FGVC
- nlp
- Vision
- GAN
- Python
- 자료구조
- algorithm
- web
- Torch
- 알고리즘
- Depth estimation
- nerf
- computervision
- Front
- cs
- CV
- REACT
- 머신러닝
- PRML
- 딥러닝
- classification
- Today
- Total
KalelPark's LAB
[ Algorithm ] Heap & Priority Queue? 본문

Heap 이란?
완전 이진트리(Complete Binary Tree)의 일종으로 우선순위 큐를 위하여 만들어진 자료구조이다.
여러 개의 값들 중에서 최댓값이나 최솟값을 빠르게 찾아내도록 만들어진 자료구조이다.
힙은 일종의 반정렬(느슨한 정렬 상태) 상태를 유지합니다.
- 큰 값이 상위 레벨에 있으며, 작은 값은 하위 레벨에 있다고 보면 됩니다.
-
* Max Heaps = Max trees and also Complete binary tree
Priority Queue 이란?
큐(Queue)는 먼저 들어오는 데이터가 먼저 나가는 FIFO(First in First Out 형식의 자료구조 이다.
우선순위 큐(Priority Queue)는 일반적으로 힙(Heap)을 이용하여 구현합니다.
일반적으로, insertion과 deletion을 하는 경우 시간복잡도가 O(logN)이다.
하지만, tree가 unbalanced하는 경우, 시간복잡도는 O(N)입니다.
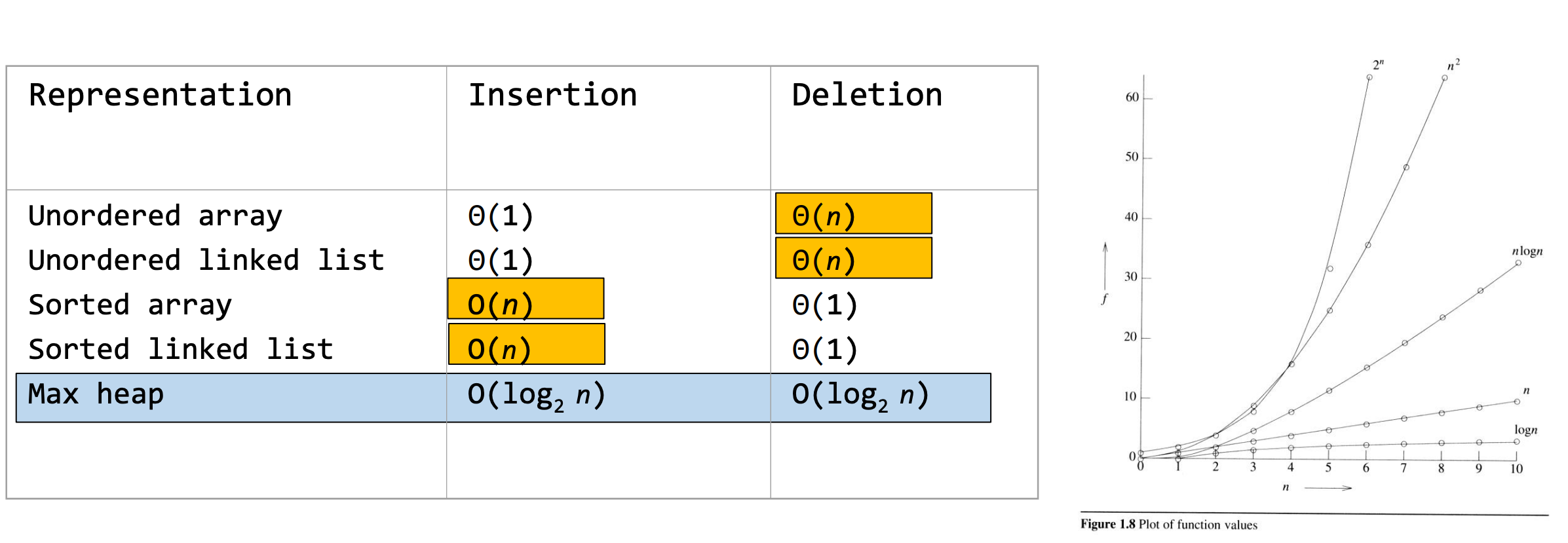
Priority Queue 동작
1. 노드를 트리에 삽입하는 경우, 완전 이진트리를 유지하는 형태로 순차적으로 삽입합니다.
2. 노드를 트리에 삽입한 이후, 루트 노드까지 거슬러 올라가면서, 최소 힙 혹은 최대 힙을 구성합니다.
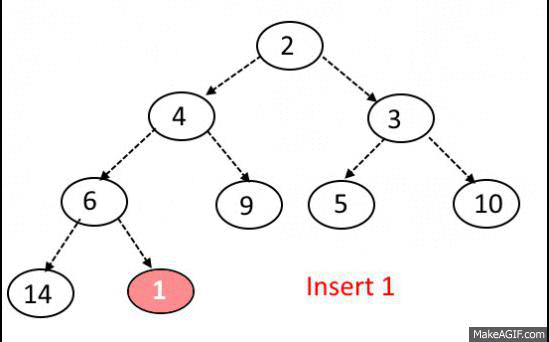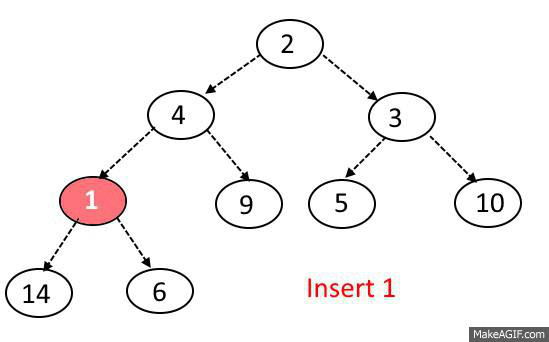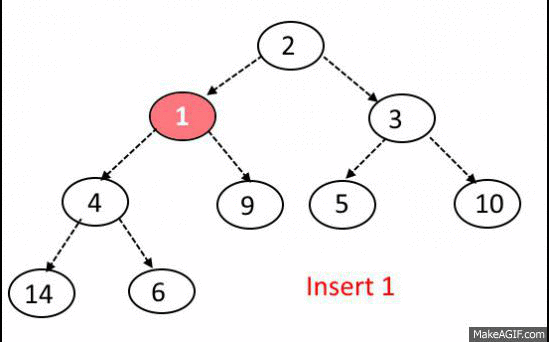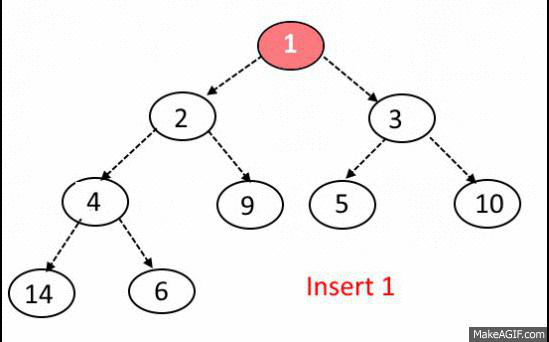
Priority Queue code with C/C++
Insertion into a Max Heap code
#define MAX_ELEMENTS 200
#define HEAP_FULLL(n)
#define HEAP_EMPTY(n)
typedef strcut {
int key;
} element;
element heap[MAX_ELEMENTS];
int n = 0;
void push(element item, int *n) { // Insertion into a Max Heap
int i;
if (HEAP_FULL(*n)) {
fprintf(stderr, "the heap ios full. \n");
exit(EXIT_FAILURE);
}
i = ++(*n);
while ((i != 1) && (item.key > heap[i/2].key)) {
heap[i] = heap[i/2];
i /= 2;
}
heap[i] = item;
}Deletion from a Max Heap code
element pop(int *n) {
int parent, child;
element item, temp;
if (HEAP_EMPTY(*n)) {
fprintf(stderr, "The heap is empty. \n");
exit(EXIT_FAILURE);
}
item = heap[1];
temp = heap[(*n)--];
parent = 1;
child = 2;
while (child <= *n) {
if ((child < *n) && (heap[child].key < heap[child+1].key))
child++;
if ( temp.key >= heap[child].key)
break;
heap[parent] = heap[child];
parent = child;
child *= 2;
}
heap[parent] = temp;
return item;
}
'Study > Algorithm' 카테고리의 다른 글
| [ Algorithm ] Merge Sort, Heap Sort? (0) | 2022.12.05 |
|---|---|
| [ Algorithm ] Binary Search Tree? (0) | 2022.12.04 |
| [ Algorithm ] Dijkstra's Algorithm? (0) | 2022.11.30 |
| [ Algorithm ] Insertion sort, Bubble sort, Selection sort? (0) | 2022.11.30 |
| [ Algorithm ] Bellman-Ford Algorithm이란? (2) | 2022.11.29 |
Comments




