| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 |
- pytorch
- Vision
- math
- dl
- 3d
- clean code
- 알고리즘
- web
- ML
- Meta Learning
- computervision
- FGVC
- nlp
- Depth estimation
- nerf
- 머신러닝
- Python
- REACT
- GAN
- 자료구조
- Front
- SSL
- PRML
- algorithm
- 딥러닝
- classification
- CV
- FineGrained
- Torch
- cs
- Today
- Total
KalelPark's LAB
[ Algorithm ] Bellman-Ford Algorithm이란? 본문

Bellman-Ford Algorithm 이란?
한 정점(Vertex)에서 다른 정점(Vertex)까지의 최단 거리를 구하는 알고리즘이다. 다익스트라(Dijkstra Algorithm)과 달리,
정점(Vertex) 간의 간선(edge) 비용이 음수인 경우에도 사용가능하다.
벨만 포드(Bellman-Ford)는 다이나믹 프로그래밍(Dynamic Programming)이라고도 할 수 있다.
그러한 이유는 매번 저장해놓은 최소 비용을 활용해서, 새로운 최소 비용을 갱신하기 때문이다.
벨만 포드(Bellman-Ford)는 다익스트라(Dijkstra Algorithm)보다 시간이 오래 걸리는데, 그러한 이유는 최소 비용을 가지는
간선(edge)만을 우선적으로 뽑는 다익스트라(Dijkstra Algorithm) 달리, 음의 간선(edge)때문에,
모든 경우의 수를 전부 탐색하는 알고리즘이기 때문이다.
벨만 포드(Bellman-Ford)의 시간 복잡도는 O(VE) 이다.
Bellman-Ford Algorithm 동작
1. 시작 정점을 선택합니다.
2. 모든 간선들을 탐색하면서, 시작 정점(Vertex)에서 다른 정점(Vertex)까지의 거리를 갱신합니다.
(이러한 과정을 Vertex의 수 - 1만큼 진행합니다.)
3. 만약 음의 사이클을 발견하였다면, 최단경로가 존재하지 않는다고 합니다.
(확인 방법 : V - 1개의 간선(Edge)보다 더 많은 (Edge)를 통하여, 최단경로를 구하는 것이 가능하면,
음의 사이클이 존재한다고 판단가능합니다.)
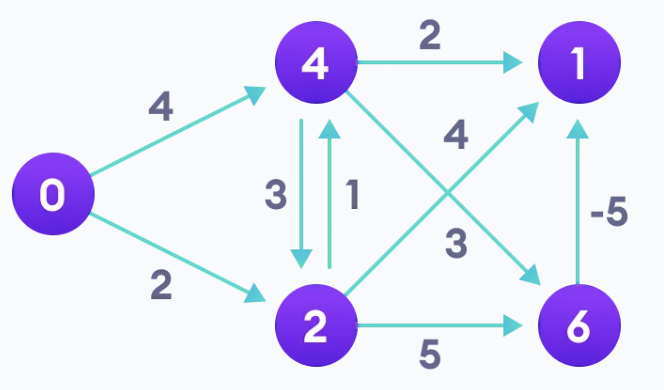
Bellman-Ford Algorithm의 구체적인 원리
1. 시작 정점(Vertex)을 선택합니다. (0을 기준으로 하겠습니다.)
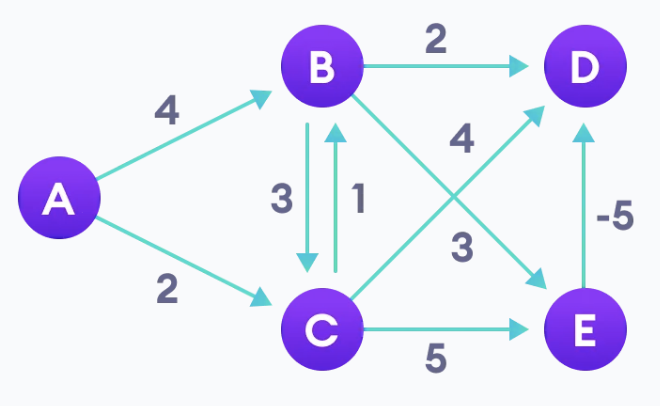
2. 정점(Vertex)을 선택하고, 다른 정점(Vertex)에 경로 값을 INF로 초기화합니다.
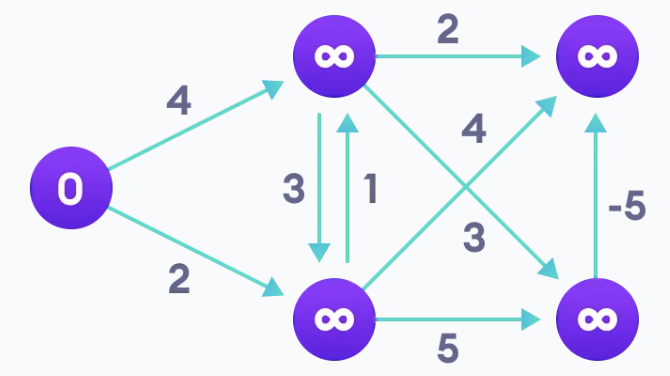
3. 각각의 간선(Edge)을 활용하여 방문하고, 거리를 파악합니다.
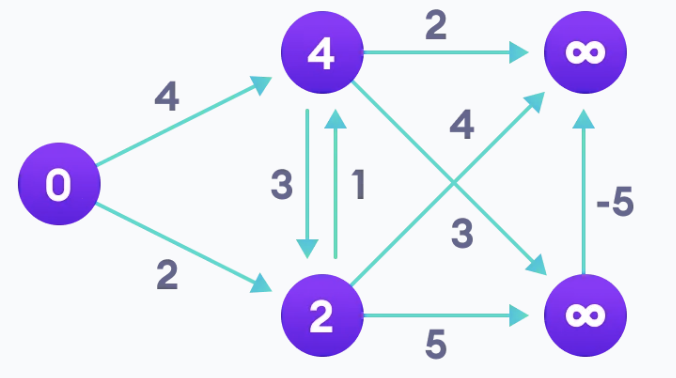
4. 간선(Edge)의 연결을 통하여, 인접하지 않지만, 가까운 정점(Vetex)을 방문합니다.
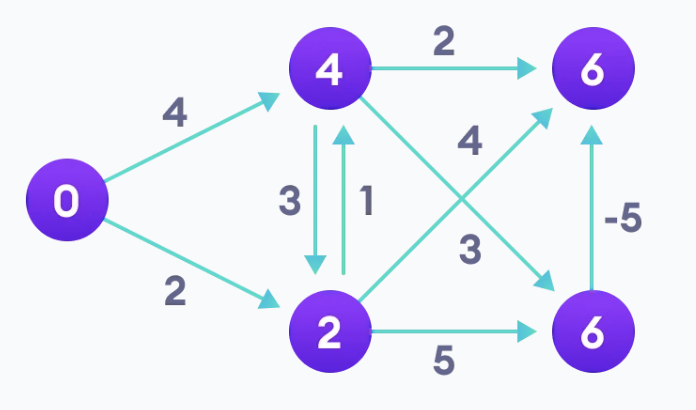
5. 음의 간선을 활용하여, 비용이 최소화가 가능한 것이 있다면, 최대한 최소화합니다.
Bellman-Ford Algorithm Pseudo code
void BellmanFord(int n, int v) {
// 한개의 정점에서, 나머지 정점에서 방문할 수 있는 최소의 거리
for (int i = 0; i < n; i++)
dist[i] = length[v][i]; // 거리 초기화
for (int k = 2; k <= n-1; k++)
for (자신의 정점과 다른 정점을 한가지 선택합니다.)
for (each <i, u> in the edge)
if (dist[u] > dist[i] + length[i][u])
dist[u] = dist[i] + length[i][u];
for (각 정점사이에 간선의 여부 파악) // 음의 사이클 여부 파악
if (dist[w] > dist[u] + length[u][w])
return False;
}Bellman-Ford Algorithm with C/C++
// Bellman Ford Algorithm in C
#include <stdio.h>
#include <stdlib.h>
#define INFINITY 99999
struct Edge {
int u; //start vertex of the edge
int v; //end vertex of the edge
int w; //weight of the edge (u,v)
};
//Graph - it consists of edges
struct Graph {
int V; //total number of vertices in the graph
int E; //total number of edges in the graph
struct Edge *edge; //array of edges
};
void bellmanford(struct Graph *g, int source);
void display(int arr[], int size);
int main(void) {
//create graph
struct Graph *g = (struct Graph *)malloc(sizeof(struct Graph));
g->V = 4; //total vertices
g->E = 5; //total edges
//array of edges for graph
g->edge = (struct Edge *)malloc(g->E * sizeof(struct Edge));
//------- adding the edges of the graph
/*
edge(u, v)
where u = start vertex of the edge (u,v)
v = end vertex of the edge (u,v)
w is the weight of the edge (u,v)
*/
//edge 0 --> 1
g->edge[0].u = 0;
g->edge[0].v = 1;
g->edge[0].w = 5;
//edge 0 --> 2
g->edge[1].u = 0;
g->edge[1].v = 2;
g->edge[1].w = 4;
//edge 1 --> 3
g->edge[2].u = 1;
g->edge[2].v = 3;
g->edge[2].w = 3;
//edge 2 --> 1
g->edge[3].u = 2;
g->edge[3].v = 1;
g->edge[3].w = 6;
//edge 3 --> 2
g->edge[4].u = 3;
g->edge[4].v = 2;
g->edge[4].w = 2;
bellmanford(g, 0); //0 is the source vertex
return 0;
}
void bellmanford(struct Graph *g, int source) {
//variables
int i, j, u, v, w;
//total vertex in the graph g
int tV = g->V;
//total edge in the graph g
int tE = g->E;
//distance array
//size equal to the number of vertices of the graph g
int d[tV];
//predecessor array
//size equal to the number of vertices of the graph g
int p[tV];
//step 1: fill the distance array and predecessor array
for (i = 0; i < tV; i++) {
d[i] = INFINITY;
p[i] = 0;
}
//mark the source vertex
d[source] = 0;
//step 2: relax edges |V| - 1 times
for (i = 1; i <= tV - 1; i++) {
for (j = 0; j < tE; j++) {
//get the edge data
u = g->edge[j].u;
v = g->edge[j].v;
w = g->edge[j].w;
if (d[u] != INFINITY && d[v] > d[u] + w) {
d[v] = d[u] + w;
p[v] = u;
}
}
}
//step 3: detect negative cycle
//if value changes then we have a negative cycle in the graph
//and we cannot find the shortest distances
for (i = 0; i < tE; i++) {
u = g->edge[i].u;
v = g->edge[i].v;
w = g->edge[i].w;
if (d[u] != INFINITY && d[v] > d[u] + w) {
printf("Negative weight cycle detected!\n");
return;
}
}
//No negative weight cycle found!
//print the distance and predecessor array
printf("Distance array: ");
display(d, tV);
printf("Predecessor array: ");
display(p, tV);
}
void display(int arr[], int size) {
int i;
for (i = 0; i < size; i++) {
printf("%d ", arr[i]);
}
printf("\n");
}Author's GitHub
'Study > Algorithm' 카테고리의 다른 글
| [ Algorithm ] Heap & Priority Queue? (0) | 2022.12.04 |
|---|---|
| [ Algorithm ] Dijkstra's Algorithm? (0) | 2022.11.30 |
| [ Algorithm ] Insertion sort, Bubble sort, Selection sort? (0) | 2022.11.30 |
| [ Algorithm ] Sollin's Algorithm 이란? (0) | 2022.11.28 |
| [ Algorithm ] Prim's Algorithm 이란? (0) | 2022.11.28 |




