[ Math ] chapter 2.1 [Image Formation]

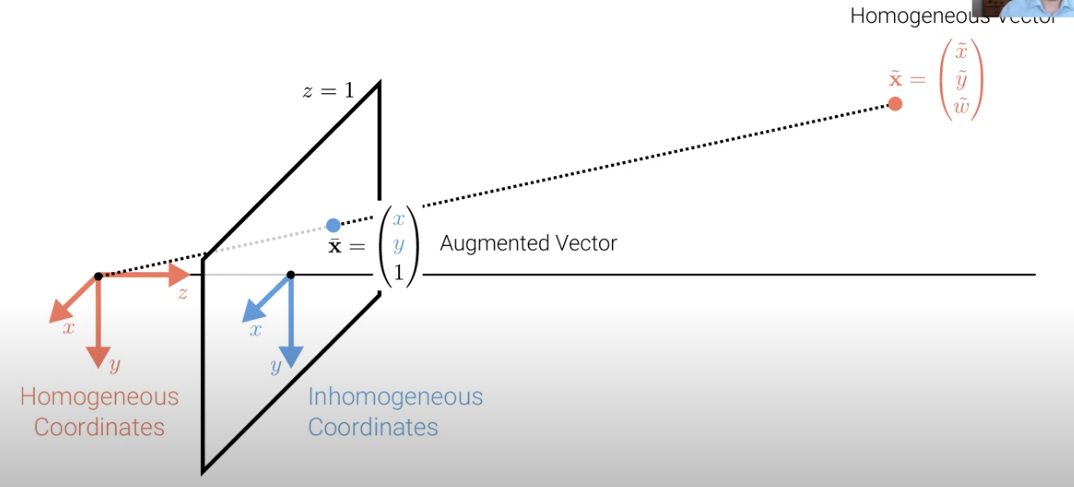
동치 좌표(homogeneous coordinates)

        - 변환 등 어떤 목적을 위해 3차원 좌표를 한 치수 올리거나, 한 치수 내릴 때 사용하는 표현

           (2차원 좌표를 3차원 좌표에 뿌려도 동일하다는 것)

          = 동차 좌표계상 변환된 좌표 = 로컬 좌표계의 P * 월드 행렬 * 카메라 행렬 * 투영 행렬

 

        - 동차 좌표계와 일반적인 3차원 좌표계의 관계
            (x, y, z, w) = (x/w, y/w, z/w, 1) : 결국 3차원 좌표계도 w값이 1인 동차 좌표계

        - 벡터를 포인트 혹은 벡터로 활용하기 위해서, 변환된 벡터를 3D 벡터의 동치벡터로 전환
Ref  : https://m.blog.naver.com/jsjhahi/199987246

2D Lines

외적을 이용하여, 선분과 선분의 교차점 구하기 : https://bowbowbow.tistory.com/17

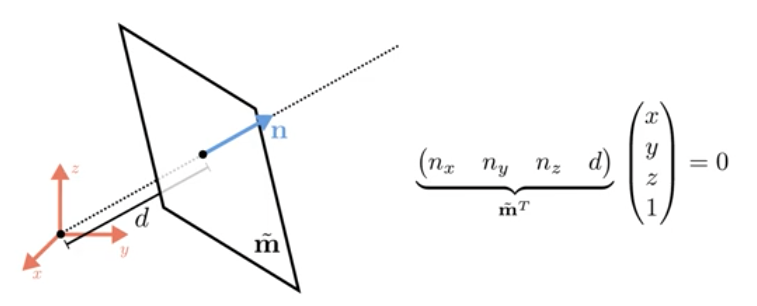
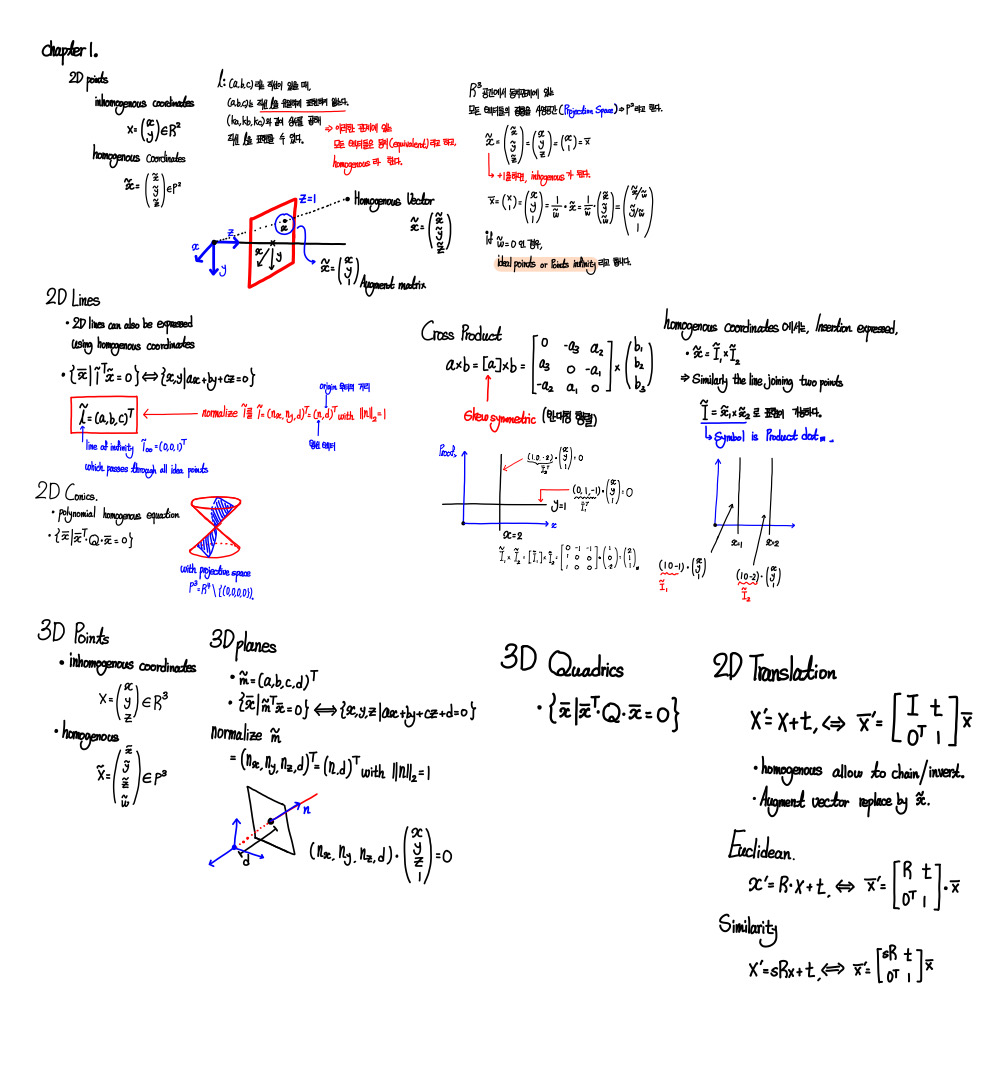
3D Planes , 3D Points

 

 

Reference

https://i-am-eden.tistory.com/56

[Tübingen ML] Computer Vision Lecture 정리

 

https://youtu.be/NIaICLR7D0Q

https://wjdgh283.tistory.com/entry/%EC%A7%81%EC%84%A0%EA%B3%BC-%EC%A7%81%EC%84%A0%EC%9D%98-%EA%B5%90%EC%B0%A8%EC%A0%90-%EA%B5%AC%ED%95%98%EA%B8%B0

직선과 직선의 교차점 구하기